sin・cos・tan、三角比・三角関数の基礎をスタサプ講師がわかりやすく解説！

三角比・三角関数を攻略するためには、sin・cos・tan（サイン・コサイン・タンジェント）の値を確実に求められるようになることが重要だ。

また、有名角の三角比を自由自在に使えるようになることが特に重要なので、しっかりと学習してほしい。

さらに、相互関係の公式を利用して、三角比を求めていくことも三角比・三角関数の問題を解いていくために基本的な学習事項なので、問題を解きながら覚えてほしい。

まずは、三角比の基本を中心に詳しく解説していこう。今回解説してくれるのは
スタディサプリ高校講座の数学講師 山内恵介先生
上位を目指す生徒のみならず、数学が苦手な生徒からの人気も高い数学講師。
数多くの数学アレルギー者の蘇生に成功。
緻密に計算された授業構成と熱意のある本気の授業で受講者の数学力を育てる。
厳しい授業の先にある達成感・感動を毎年数多くの生徒が体験！

著書に、『「カゲロウデイズ」で中学数学が面白いほどわかる本』、『「カゲロウデイズ」で中学数学が面白いほどわかる本［高校入試対策編］』、『ゼッタイわかる 中1数学』、『ゼッタイわかる 中2数学』、『ゼッタイわかる 中3数学』（以上、KADOKAWA）監修。三角比で使われるsin(サイン)・cos(コサイン)・tan(タンジェント)とは

サインやコサイン、タンジェントとは三角比とよばれるものだ。

直角三角形の直角とそれ以外の角度が1つわかると、三角形の辺の長さの比が決まる。

このときの三角形の辺の２つの辺の比のことを三角比と言う。

ある1つの基準となる角度に対して、どの辺とどの辺を使った三角比なのかによって、サイン、コサイン、タンジェントと呼び方が変わってくる。

ちなみに、三角形の3つの角度が同じで、大きさの違う三角形は同じ三角比をもつ。

つまり、２つの相似な三角形は同じ三角比をもつということになる。

古代から大型の建物や橋を建造するときや、長い距離を計算したり、遠くからやってくる海賊船と自分のいる場所までの距離を計算したりといった様々な場面で、三角比を使った計算が利用されてきた人類の歴史がある。

人間の力では計測できないような大型の建築物や長い距離でも、机の上に書いた三角形が、それらの巨大な建築物や長い距離と相似な三角形になっていれば、三角形の三角比を使った計算式で高さや距離が分かってしまうという非常に優れた計算方法だったようだ。直角三角形の中でsin(サイン)・cos(コサイン)・tan(タンジェント)の値を求められるようになろう

直角三角形の中で三角比を求めるために、以下のような直角三角形を書いて考える。

上記の直角三角形は、左下に「基準となる角」、右下に直角が来るように書いている点。

さらに、直角三角形の辺に上記のように名前をつける。

・「基準となる角度と向かい合っている辺」を「対辺（読み方：たいへん）」

・「直角と向かい合っている辺」を「斜辺（読み方：しゃへん）」

・「基準となる角と直角を両端にもつ辺」を「隣辺（読み方：りんぺん）」

まずは、直角三角形の中から、対辺、斜辺、隣辺を見つけられるように練習してほしい。

対辺、斜辺、隣辺という言葉も使いながら、三角比の見つけ方をさらに詳しく紹介していこう。

直角三角形におけるsin(サイン)の値の求め方

直角三角形において、サインの値を求める方法を紹介しよう。

上記のように、基準となる角を左下、直角を右下に書いた直角三角形を用意しよう。

基準となる角の大きさをθ（シータ）とする。

サインの値を求めるときに使う2つの辺は「斜辺」と「対辺」である。

角θのサインの値をsinθ（サインシータ）と表し、

と求める。上記の直角三角形では
である。

斜辺の長さを分母、対辺の長さを分子とする分数の値がサインの値だ。

ちなみに三角比は通常、sin●のように、sinやcos、tanに具体的な角度の値を一緒に書く。

慣れるまでは、「基準となる角が左下」で「直角が右下」にくる直角三角形を書いて考えるとよい。

直角三角形におけるcos(コサイン)の値の求め方

次に、直角三角形において、コサインの値を求めていこう。

コサインの値を求めるときに使う2つの辺は「斜辺」と「隣辺」である。

角θのコサインの値をcosθ（コサインシータ）と表し、

と求める。上記の直角三角形では
である。斜辺の長さを分母、隣辺の長さを分子とする分数の値がコサインの値だ。

直角三角形におけるtan(タンジェント)の値の求め方

最後に、直角三角形において、タンジェントの値を求めていこう。

タンジェントの値を求めるときに使う２つの辺は「隣辺」と「対辺」である。

角θのタンジェントの値をtanθ（タンジェントシータ）と表し、
と求める。上記の直角三角形では
である。隣辺の長さを分母、対辺の長さを分子とする分数の値がタンジェントの値だ。

直角三角形をかいて三角比の値を求めていくことは、基本かつ重要なことなので、しっかりと学習して慣れてほしい。

三角比の重要公式「三角比の相互関係」について

三角比の基本でもあり重要公式である「三角比の相互関係」。

３つの公式と、その使い分けについて説明していく。

三角関数の基本的な知識や注意点について

さきほども紹介したが、sinやcos、tanは必ず基準となる角の大きさとセットで使わなくてはならない。

また、サインやコサイン、タンジェントの値を2乗する場合の表記の仕方にも気をつけよう。

例えば、sinθの値を２乗した値（sinθ)２はsin2θのように指数２を右上に書く。

sinθ２としてしまうとθ２のサインを表すことになってしまうので注意！

「三角比の相互関係」の公式その1

サインかコサインの値のうち、どちらか一方が分かっている場合に使える相互関係の公式がある。

サインの値が分かっているときにはコサインの値がこの公式で求められる。
同様に、コサインの値が分かっているときには、サインの値がこの公式で求められる。

実際には「基準となる角度がどの範囲の角度なのか」によって、答えの符号が決まるので、基準となる角度の範囲をしっかりと確認して答えを出せるようにしておくとよいだろう。

直角三角形で三角比を考えるときはθは鋭角（０゜＜θ＜９０゜）であり、サイン、コサイン、タンジェントはすべて正（＋）である。

今後、θの範囲を広げていくと、三角比の値が０や－（マイナス）になることがあるので、注意が必要である。

参考として、基準となる角度の範囲と三角比の符号の関係性について、表でまとめておくので、しっかりと理解しておこう。

0°＜θ＜90°90°＜θ＜180°

サインの符号＋＋

コサインの符号＋―

タンジェントの符号＋―

最後に、相互関係の公式その1の証明も紹介しておこう。

証明には、サインの値が斜辺と対辺の長さ、コサインが斜辺と隣辺の長さで求められることを応用させていく。

さらに「三平方の定理」も利用して証明していくことになるので、三平方の定理についても確認しておこう。

証明は以下のとおり。

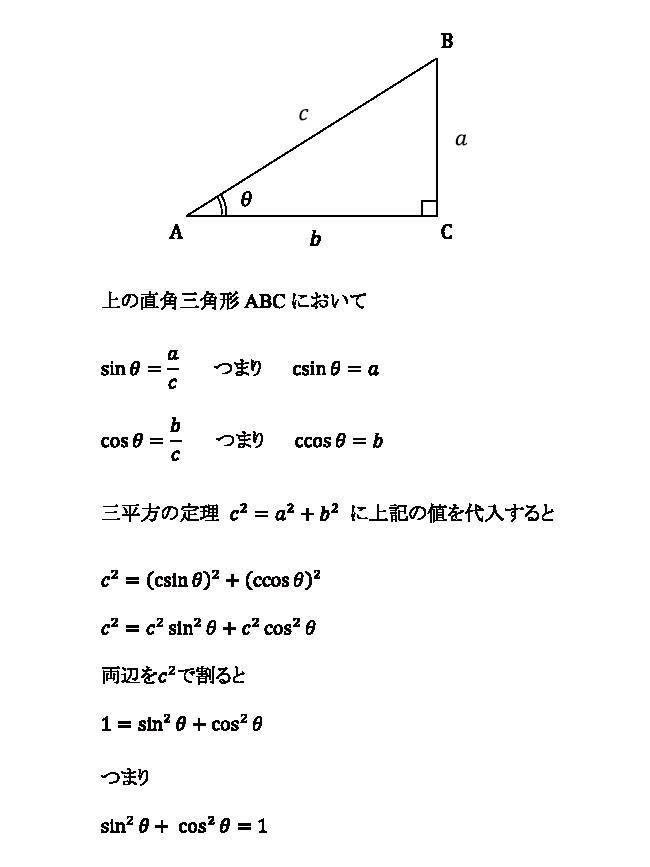
証明の方法を覚えておくと、公式を忘れてしまってもその場で求めることができるので、余裕がある人は証明の方法も覚えておくことをおすすめしたい。

「三角比の相互関係」の公式その2

2つ目の相互関係の公式は、サイン、コサイン、タンジェントのうち、どれか2つの三角比の値が分かっている場合、残りの１つの三角比の値が求められるという公式だ。

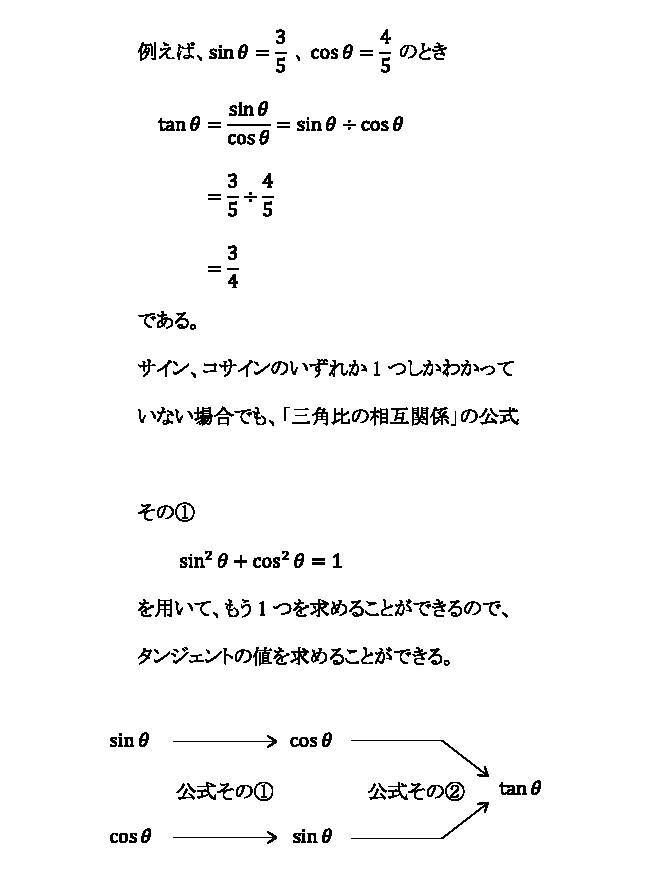
また、上記の相互関係の公式その2についても証明を掲載しておく。

公式を求めていく方法を知っておくと忘れてしまったときにその場で求められるので便利だ。

証明は以下のとおり。

「三角比の相互関係」の公式その３

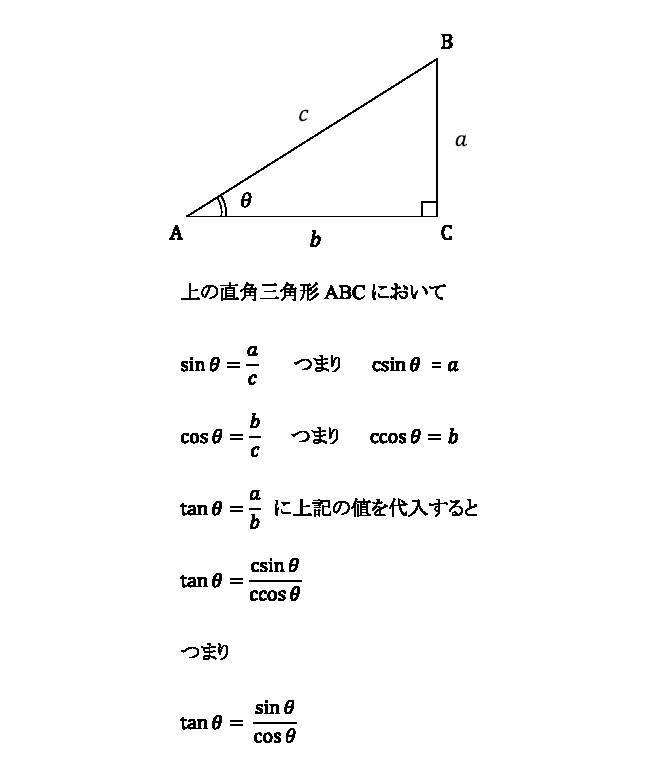
３つめの相互関係の公式は、コサインの値が分かっていればタンジェントの値が求められる公式だ。

相互関係の公式その1でも同様の話が出てきたが、「基準となる角度がどの範囲の角度なのか」によって答えの符号が決まるので、基準となる角度の範囲をしっかりと確認して答えを出せるようにしておこう。

また、三角形の相互関係の公式その①を用いれば、cosθの値かを求めることができる。

また、公式の証明についても紹介しておこう。

三角比攻略の鍵！2つの直角三角形の三角比を完璧に理解しよう！

三角比の中でも特によく使うものとして、有名角を基準とした三角比がある。

有名角とは、鋭角（０°から90°の間の角）においては30°、45°、60°である。

これら、有名角を内角にもつ直角三角形は三角比ではよくでてくる。以下でより詳しく紹介していこう。

超重要な２つの直角三角形について

上記の２種類の直角三角形は小学校や中学校でおなじみの直角三角形である。

実は、この２つの直角三角形は基準となる角がわかれば、辺の長さがわからなくてもサイン、コサイン、タンジェントの値がわかる、非常に重要な直角三角形なのだ。

「三平方の定理」で、この２つの直角三角形の「辺の比」を覚えたと思う。
では、この２つの直角三角形で有名角の三角比を求めていこう。

なお、以下の図では、左下に基準となる角、右下に直角がくるように設定している。
これらの三角形の値を丸暗記するのではなく、３つの辺の比をイメージしながら、なぜこの値になるのかとセットで覚えていこう。

三角比は広がっていく

三角比は、xy平面の力を借りて、基準となる角度が 90° 以上の場合でも考えていくことができる。

三角比では０°から180°の角を、そして「三角関数」では180°より大きい角などに広がっていく。

この方法で値を見つけていくと、下記の表の値をすべて埋められるようになる。

以下では、参考までに０°から180°までの有名角と、その三角比の値を示す。

30°、45°、60°の三角比の値と同様に、これらの値を、丸暗記ではなく「なぜそうなるのか」を考え、値をいつでも出せるようにしておこう。

また、この表の中の値は、その後の三角比や三角関数の問題を解くうえで非常によく使う値なので、それまでにしっかり覚えておこう。

sin(サイン)・cos(コサイン)・tan(タンジェント)の基本的な考えや公式を使いこなして三角比・三角関数を攻略せよ！

直角三角形を使ってサイン、コサイン、タンジェントといった三角比の値を求めていく方法から、与えられた三角比の値から他の三角比の値を見つける相互関係の公式、有名角を基準となる角としてもつ直角三角形を使った三角比の値の求め方について紹介していった。

三角比や三角関数の問題を解いていくうえで、三角比の値は計算の道具だ。

ただし、その道具がどのように生まれ、どのような意味をもつ道具なのかを理解してこそ、真価を発揮するものだ。

その道具の使い方や使い時がわかり、また、万が一のときには自分でもう一度その道具を生み出すこともできる。

道具である三角比の値を使って、さまざまな三角比や三角関数の問題に挑戦していってもらいたい。

また、三角関数につながる考え方として、単位円を使って三角比を求める方法も是非とも学習してほしい。

今回紹介した三角比の知識は超基本。

使える知識として身につけることが三角比・三角関数攻略には必須なのだ。

構成・文／スタサプ編集部 監修／山内恵介 イラスト／てぶくろ星人

★教材付き＆神授業動画でもっと詳しく！