【小学生で教わる割り算なのに…超ムズい】1÷0の答はナニ？答えられそうで詰まってしまう…その答とは？

割り算は小学校3年生で習いますが、0を使う割り算って、意外と奥が深いのをご存じですか？ちょうど去年、小学校の算数プリントで「18÷0＝答えなし」と回答して、バツがつけられたというX（旧Twitter）のポストが話題になりましたよね。そんなことも踏まえ、ここで問題。0÷1＝0ですが、1÷0の答えはいくつになるでしょう？そんなのあれこれ考えることなく、計算機を使えば一瞬でしょと思いきや…。

『骨の数ってな、206あんねん』（byアンミカ!?）…でもな、子供の骨はもっとあんねん！さて、いくつある!?

【問題】1÷0の答えはいくつになるでしょう？

はるか昔、わたしが小学生の頃、0÷1のような割られる数が0の計算をした覚えはあるものの、割る数が0の計算って、教えてもらった記憶がないのだけど…。みなさんはどうですか？

thinking time

↓

↓

↓

正解は…。

計算機に1÷0を入れてみると、


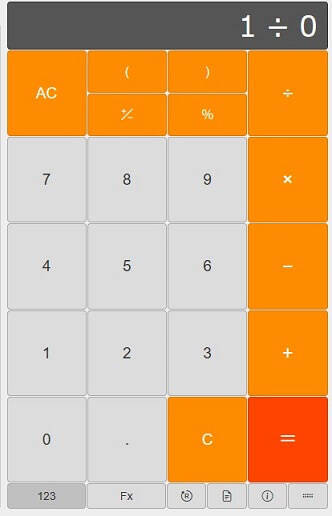
画像出典: 「WEB電卓」

ジャン！


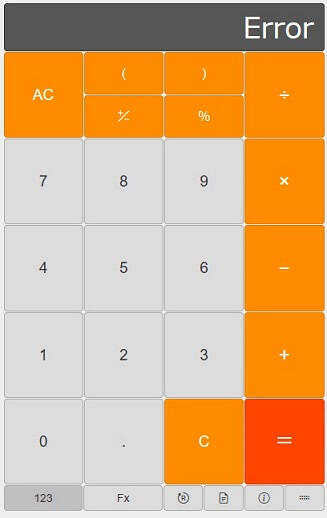
画像出典: 「WEB電卓」

「Error」

えっ、え、え、え、エラー!?

エラーとはどういうことなのでしょう？

先ほど触れた、去年話題になったX（旧Twitter）の投稿にあった、「18÷0＝答えなし」のように、「1÷0＝答えなし」が正解なのでしょうか？

そのX（旧Twitter）のポストというのが、ちゃーろー@カメレオン絵師さんのこちらのポスト。

半分炎上してた娘（8歳）の小学校の、プリントが返ってきたので報告します。

【18÷0＝】を【こたえなし】

で提出したら。
先生ににされて【0】だと言われたそうです。

割り算に0が入ると全て0らしい。

これで本当にいいんやろうか…割れませんよね…？ pic.twitter.com/VLWhUmSpuA— ちゃーろー@カメレオン絵師 (@charlow_illust) June 18, 2024
8歳の娘さんが、小学校の算数プリントで、「18÷0＝こたえなし」と回答したところ、先生にバツをつけられ、答えは「0」と言われたそうです。

先生は「割り算に0が入ると全て0」と、単純明快なものの、あまり数学的ではない説明をしたそうです。

このポストに対し、「0で割ることは出来ないはず」「答えは0ではない」など、いろいろな意見が相次ぎ、8.2万いいね！がつくほど注目されたんです。

現役の数学の先生や元校長先生から、「数学教員ですが、0で割ること自体がダメです。検算をするとよくわかります。その検算がおかしくなりますので…」「数学科教員です。算数の範囲であれば『こたえなし』が正しいと思われます。小学校は基本科目を1人の教員が行うので、その先生が数学苦手だった場合もありえます。先生のことはあまり強く責めないであげてくださいね」「元小学校校長です。これは小学校で指導する範囲ではないので、きちんと説明を求めた方がいいと思います」といったコメントもありました。

投稿者のちゃーろー@カメレオン絵師さんは、「割り算に0が入ると全て0」と言った先生を責めようと思ってポストしたのではなく、「18÷0＝0」とする理由を先生に聞いてみたくて電話しようとしたら、”モンペ”になるからと娘さんと奥様に止められ、ポストすることにしたそうです。

小学校の元校長先生も「小学校で指導する範囲ではない」と言っているし、みなさんも、「18÷0＝0」と指導した先生を温かい目で見てあげましょうね。

…と、余談はさておき、本日の本題、1÷0の答えは、どうやら「答えなし」となるみたいです。

でもなぜ、「答えなし」なんでしょう？

頼りになる、わが心の友、「Gemini」に聞いてみると…、


画像出典:Google「Gemini」

「1÷0の答えは、定義されません。数学において、ゼロで割ることはできません。もしゼロで割ることができたと仮定すると、矛盾が生じてしまいます。」とのことでした。

「定義されない」「数学において、ゼロで割ることはできない」って???

なんだか、よくわからないので、「1÷0」について、深掘りすることに！

「0で割る」とはどういうこと？


画像出典:photoAC

そもそも、数字を0で割るとはどういうことなんでしょう？

式が1÷0になる問題文を作ってみると、「りんごが1個あります。これを0人で分けたら、1人あたり何個のりんごがもらえますか？」となります。

日本語的にも、おかしな問題文です。

”0人で分ける”…。そんなことありえません。

問題文として成り立たないから、計算のしようもない。だから「答えはなし」ということ？

けれど、0人で分けるということは、誰の手にも渡らないから、答えは0かもしれないし、分けないから答えは1とも言えるかも。

モヤモヤがとれないので、別のアプローチで考えてみましょう。

割り算は、かけ算の「逆演算」であると定義されていることに注目。

6÷3＝2　→　2×3＝6　となりますよね。

これに1÷0を当てはめてみると（1÷0の答えを仮に●とします）、

1÷0＝●　→　●×0＝1

●に何が入るのか考えてみます。

「0は何倍しても0」という0の定義があるので、●にどんな数字を入れても、この式を成立させることはできない、とわかります。

つまり、「答えなし」というわけ。これを数学用語では「不能」というそうです。「不能」とは「解を求めることができない（存在しない）」という意味らしいです。

ただ、0で割る式「●÷0」の中で、解が「不能」にならないものが、1つだけあるそうです。

それはなんだかわかりますか？

そうです！

0÷0

同じようにかけ算で考えてみると（1÷0の答えを仮に●とします）、

0÷0＝●　→●×0＝0

先ほどとは真逆で、●にどんな数字を入れても式が成立するのです。

0÷0の答えは数学用語では「不定」というそうです。「不定」とは「解が1つに定まらない」という意味。

0÷0＝不定　となるわけです。

●をaに置き換え、数学っぽくまとめると、

a÷0のとき、a≠0であれば、答えは「不能」となる
a÷0のとき、a=0すなわち0÷0であれば、答えは「不定」となる　というわけです。

計算の答えが数字ではなく、「不能」「不定」と漢字で表されるのは新鮮ですよね。

このように「0で割る」場合の答えは、「不能」もしくは「不定」となりますが、こんな考え方もあるそうです。

高校の数学Ⅲに「関数の極限」という単元があり、「極限」とは「限りなくある数に近づけていく」という考え方だそうです。

数学脳のないわたしには、ちんぷんかんぷんでしたが、この考え方に従って、高校3年生レベルではなく、噛み砕いて、噛み砕いて小学生レベルで簡単に考えてみました（笑）。たぶん、間違っていないと思うけど…。

1÷0＝●　→　●×0＝1　となるのは先ほどやりましたよね。

「●×0＝1」の「0」を”0に近い数”にして計算してみます。

例えば「0.01」にすると、

●×0.01＝1　●＝100　となります。

さらに、”0に近い数”を入れてみると…。

●×0.001＝1　　●＝1000　
●×0.0001＝1 　●＝10000
●×0.00001＝1  ●＝100000

というように、割る数を0に近づけるほど、答えはどんどん大きくなっていきます。これを永遠に行うと、億、兆、京と位が上がっていき、最終的には無限大になることが予想されます。これを数学用語で、「無限大に発散する」と言うそうです。

1÷0の解は「不能」であり、「数字を0で割る」ことはできませんが、割る数が0に近ければ近いほど、答えが大きくなることがわかります。

「0で割ることはできない」の一言で終わらせてしまうのは簡単ですが、いろいろな視点で考えてみることって大切で、そこに”考える”楽しさがあるのかなと感じました。夏休みに、計算問題をただ解くだけでなく、お子さんと算数・数学の「なぜ？」を見つけ、一緒に考えてみるのも楽しそうですね。

＜参考文献＞
WEB
『ゴリラティーチャー教壇に立つ～なぜ÷0は計算できない？0で割れない理由をわかりやすく解説～』
https://gorilla-teacher.com/division-zero/